在人类早期的认知里，数学是简单而纯粹的，整数被视为宇宙万物的完美表达。

古希腊的毕达哥拉斯学派更是将 “万物皆数” 的理念奉为圭臬，他们坚信所有的数都能表示为整数或整数之比，数学的和谐与完美就体现在这些简洁的数字之中。

这种对整数的崇拜，源于人们对自然规律简洁性的追求，认为整数的规律性和确定性能够解释世间一切现象。

然而，希帕索斯的发现如同一颗重磅炸弹，打破了这种美好的幻想。当他在研究等腰直角三角形时，发现若直角边为 1，根据勾股定理，斜边长度为根号2。

但无论怎样尝试，他都无法将根号2表示为整数或整数之比。这一发现不仅挑战了毕达哥拉斯学派的核心教义，也冲击了当时人们对数学的普遍认知，因为在他们的观念里，所有的量都应该可以用有理数精确表示。

希帕索斯的发现引发了巨大的恐慌和争议，他本人甚至因此遭受迫害。但无理数的存在无法被忽视，它的出现让人们开始重新审视数学的基础。与此同时，芝诺悖论的提出，进一步加深了人们对数学概念的困惑。

芝诺悖论中的 “阿基里斯追龟”“二分法” 等，通过看似严密的逻辑推理，得出了与现实经验相悖的结论，如阿基里斯永远追不上乌龟，运动的物体永远无法到达终点等。这些悖论的核心在于对无穷概念的理解和运用，它们揭示了当时人们在处理无限和连续问题时的思维困境。

面对无理数和芝诺悖论带来的挑战，古人开始深入思考无穷的概念。他们逐渐认识到，芝诺悖论中对路程的无限细分，虽然在逻辑上似乎无懈可击，但在现实中，时间是有限的，不可能在有限的时间内完成无穷多的细分步骤。这一认识为解决芝诺悖论提供了关键思路，也促使人们更加深入地研究无理数和无穷的性质。

随着对无理数和无穷概念的深入探索，人们逐渐化解了第一次数学危机。数学家们开始接受无理数作为数学的一部分，并通过建立更加严密的数学理论来处理无理数和无穷的问题。例如，欧多克斯提出的比例理论，巧妙地处理了可公度和不可公度的量，为无理数的研究奠定了基础。这一理论的出现，标志着人们对数学的认识从直观经验向逻辑推理的转变，数学的发展也由此进入了一个新的阶段。

17 世纪，科学技术的迅猛发展对数学提出了更高的要求，天文学、力学等领域迫切需要一种能够精确描述和分析连续变化现象的数学工具。在这样的时代背景下，微积分应运而生。微积分的诞生，是数学史上的一个重要里程碑，它为科学家们提供了强大的数学武器，使得许多以前难以解决的问题迎刃而解，对科学技术的发展产生了深远的影响 。

比如在天文学中，它可以精确计算行星的轨道和运动规律；在力学中，能够描述物体的运动状态和受力分析。

微积分的核心概念之一是无穷小量，它被用来描述在某个变化过程中，数值无限趋近于零的变量 。在微积分的运算中，无穷小量起到了至关重要的作用。

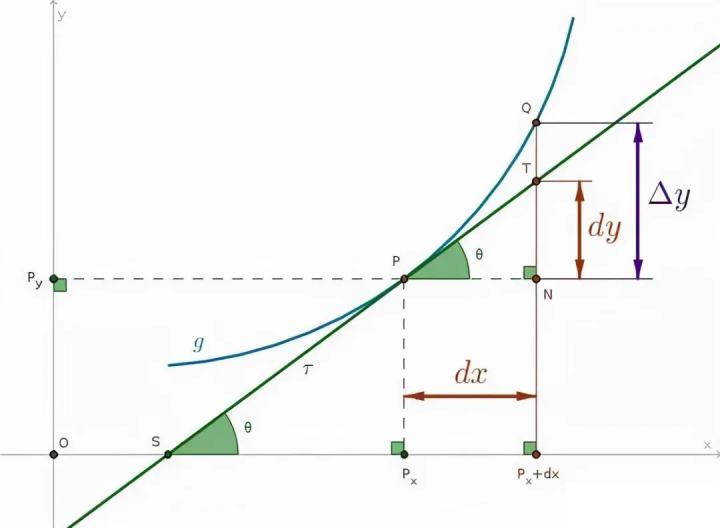
例如，在求曲线的切线斜率时，我们会在切点附近取一个边长无限小的直角三角形，用这个三角形的斜边斜率来近似替代曲线在该点的切线斜率；在计算曲边图形的面积时，我们会将图形分割成无数个无穷小的部分，然后通过对这些无穷小部分的求和来得到图形的面积。然而，无穷小量的定义和性质在当时引发了诸多争议，其中最主要的争议便是无穷小量是否为零。

在牛顿和莱布尼茨所处的时代，人们对微积分的理解还不够深入，没有完全厘清 0 和无穷小之间的关系，也未能彻底搞清楚积分、微分和导数的真正含义。以计算曲线上某点的切线斜率为例，虽然我们现在知道可以通过在切点处取一个边长无限小的直角三角形，用该三角形的斜边来近似表示切线斜率，但在当时，人们心里始终存在疑虑：无论这个直角三角形多么小，斜边与切线斜率之间似乎总是存在误差，难以完全等同。

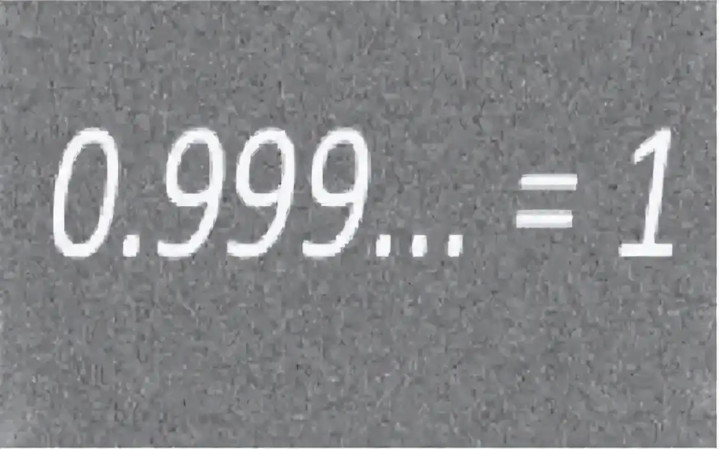
这就如同现今很多人对 “0.999...... 和 1 到底是否相等” 这一问题的质疑。从直观上看，0.999...... 似乎总是小于 1，但从数学的极限理论来分析，0.999...... 其实等于 1 。这一问题充分体现了人们在理解无穷概念时的困惑，也反映出当时微积分理论基础的薄弱。

英国大主教贝克莱于 1734 年对微积分进行了猛烈抨击，他称流数（导数）“是消失了的量的鬼魂”，认为微积分是依靠双重错误才得到了看似正确的结果。

他指出，在微积分的运算过程中，无穷小量一会儿被当作 0 来处理，一会儿又被当作非零量进行运算，这在逻辑上是自相矛盾的。贝克莱的批评并非毫无道理，当时微积分的基础确实不够严密，许多概念和运算缺乏明确的定义和逻辑依据，这使得微积分在理论上陷入了困境。

除了贝克莱，当时还有一些数学家和学者也纷纷指出微积分缺乏必要的逻辑基础，如罗尔曾说：“微积分是巧妙的谬论的汇集。” 这场围绕微积分基础定义的争论持续了长达一个半世纪之久，让数学界乃至哲学界都陷入了困惑与思考。它不仅影响了微积分的进一步发展和应用，也对整个数学的严谨性和可靠性提出了挑战。

直到 19 世纪 20 年代，一些数学家开始关注微积分的严格基础。

从波尔查诺、阿贝尔、柯西、狄里赫利等人的工作开始，到威尔斯特拉斯、狄德金和康托的工作结束，经过半个多世纪的努力，数学家们基本解决了这一矛盾，为数学分析奠定了严格的基础。

柯西重新定义了无穷小量，他指出 “当同一变量逐次所取的绝对值无限减小，以至于比任何给定的数还要小，这个变量就成为人们所称的无穷小或者无穷小量，这类变量以 0 为极限” 。这一定义使得无穷小量从一个模糊不清的概念转变为一个有着明确极限定义的变量，将其纳入了函数的范畴。在此基础上，柯西又进一步定义了连续、导数、微分、积分等概念，使微积分的这些基本概念建立在坚实的基础之上。

通过这些数学家的努力，微积分的理论基础得到了完善，第二次数学危机得以解决。微积分在坚实的逻辑基础上得以进一步发展和应用，成为了现代数学和科学技术中不可或缺的重要工具，推动了数学和其他学科的飞速发展。

20 世纪初，正当数学家们为数学大厦的日趋完善而欢欣鼓舞时，集合论中却悄然浮现出一片乌云，其引发的危机如一场风暴，席卷了整个数学界，这便是第三次数学危机。这场危机的核心，是英国数学家罗素于 1901 年提出的罗素悖论 。

罗素悖论的表述看似简单，却蕴含着深刻的逻辑矛盾。假设有一个集合 S，它由所有不属于自身的集合组成。那么问题来了，S 是否属于它自身呢？如果 S 属于 S，根据 S 的定义，S 中的元素都不属于自身，所以 S 不应属于 S；反之，如果 S 不属于 S，那么 S 就满足了集合 S 的定义，即不属于自身的集合，所以 S 又应该属于 S 。这就形成了一个无法解决的矛盾循环，如同一个逻辑的死胡同，让数学家们陷入了困境。

为了更通俗易懂地理解罗素悖论，我们可以看看 “理发师悖论” 这个有趣的例子。

在某个小镇上，有一位理发师，他打出了这样一则广告：“我将为本城所有不给自己刮脸的人刮脸，我也只给这些人刮脸。” 这听起来似乎没什么问题，但当理发师自己需要刮脸时，矛盾就出现了。

如果他不给自己刮脸，按照他的广告词，他就属于 “不给自己刮脸的人”，那么他就应该给自己刮脸；可如果他给自己刮脸，他又属于 “给自己刮脸的人”，这就违背了他 “只给不给自己刮脸的人刮脸” 的承诺。这个理发师的困境，与罗素悖论在本质上是一致的，都是由于自我指涉而产生的逻辑矛盾。

还有一个 “书目悖论”，也能帮助我们理解罗素悖论。一个图书馆编纂了一本书名词典，它列出这个图书馆里所有不列出自己书名的书。那么这本词典列不列出自己的书名呢？如果它列出自己的书名，就与它 “列出所有不列出自己书名的书” 这一规则相矛盾；如果不列出，又不符合它涵盖所有不列出自己书名的书的设定 。

这种自我指涉的逻辑矛盾并非只存在于数学和逻辑领域，在日常生活和哲学思考中也有类似的体现，比如著名的 “上帝悖论”：上帝被认为是无所不能的，那么上帝能否创造出一块他自己搬不动的石头呢？如果上帝能创造出这样一块石头，那么他就无法搬动这块石头，这与他的全能属性相矛盾；如果上帝不能创造出这块石头，那同样说明他不是全能的。这个悖论以一种极端的方式揭示了逻辑中的矛盾，与罗素悖论一样，都是对我们思维和认知的挑战。

罗素悖论的出现，如同一颗重磅炸弹，在数学界引起了轩然大波。集合论作为现代数学的重要基础，许多数学分支都是建立在集合论的基础之上。而罗素悖论的提出，揭示了集合论中存在的漏洞，使得整个数学大厦的根基受到了严重威胁。

它让数学家们意识到，看似严密的数学体系，在基础层面可能存在着致命的缺陷。正如德国著名逻辑学家弗雷格在收到罗素关于这一悖论的信时，他立刻发现，自己忙了很久得出的一系列结果却被这条悖论搅得一团糟，他只能在自己著作的末尾写道：“一个科学家所碰到的最倒霉的事，莫过于是在他的工作即将完成时却发现所干的工作的基础崩溃了。”

为了解决罗素悖论，数学家们进行了不懈的努力，提出了各种解决方案。其中，公理化集合论的出现，为解决这一危机提供了重要的思路。策梅洛 - 弗兰克尔集合论（ZF）是公理化集合论的代表性理论，它通过引入一系列公理，对集合的定义和构造进行了严格的限制，避免了自指性集合的出现，从而成功排除了集合论中出现的悖论，比较圆满地解决了第三次数学危机 。

在 ZF 集合论中，空集公理规定存在一个空集；配对公理指出对于任何两个集合，存在一个包含这两个集合的集合；并集公理表明对于任何集合，存在一个集合包含该集合内所有元素的元素；幂集公理说明每个集合都有一个幂集，即所有子集的集合。这些公理的引入，确保了集合的构造不会导致自指性问题，使得集合论更加严密和完善。